EN LA HORA 6 HE VISTO:
1ª DEFINICION DE DETERMINANTE:
Una forma multilineal alternada de un cuerpo. Esta
definición indica una serie de propiedades matemáticas y generaliza el concepto
de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el
concepto de determinante o de volumen orientado fue introducido para estudiar
el número de soluciones de los sistemas de ecuaciones lineales.
Para el cálculo de determinantes de matrices de cualquier
orden, existe una regla recursiva (teorema de Laplace) que reduce el cálculo a
sumas y restas de varios determinantes de un orden inferior. Este proceso se
puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo
de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el
determinante de un escalar es el propio escalar, es posible calcular el
determinante de cualquier matriz aplicando dicho teorema.
Además de esta regla, para calcular determinantes de
matrices de cualquier orden podemos usar otra definición de determinante
conocida como Fórmula de Leibniz.
donde la suma se calcula sobre todas las permutaciónes σ del
conjunto {1,2,...,n}. La posición del elemento i después de la permutación σ se
denota como σi. El conjunto de todas las permutaciones es Pn. Para cada σ,
sgn(σ) es la signatura de σ, esto es +1 si la permutación es par y −1 si es
impar (ver Paridad de permutaciones).
En cualquiera de los n! sumandos, el término
2ª DETERMINANTE DE UNA MATRIZ CUADRADA
El determinante de la matriz triangular vale
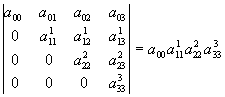
Es evidente, que el procedimiento de Gauss es posible
siempre que los elementos de la diagonal principal de la matriz transformada no
sean nulos, a estos elementos se denominan pivotes. Un procedimiento mejorado
detectará qué pivote es nulo y procederá a intercambiar una fila por otra para
evitarlo, lo que no modifica el sistema de ecuaciones, pero si el signo del
determinante.
Discutiremos, ahora, el código para reducir una matriz
cualesquiera a su matriz triangular equivalente por el método de Gauss. Tenemos
que traducir las siguientes fórmulas a código, para cualquiera que sea la
dimensión n (en el ejemplo 4) de la matriz cuadrada.
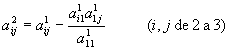 k=1
k=1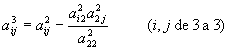 k=2
k=2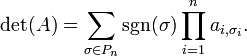
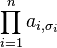

No hay comentarios:
Publicar un comentario