8ª HORA DE OPEN COURSE

En mi 8ª hora de open course e podido ver los siguientes contenidos:


RANGO DE UNA MATRIZ

Se define el rango de una matriz AÎMmxn(R) (rangA) por una de las siguientes definiciones equi-valentes:

a) Es el orden de la mayor submatriz cuadrada de A con determinante no nulo.

b) Es el mayor número de filas de A linealmente independientes.

c) Es el mayor número de columnas de A linealmente independientes.

Propiedades

i) Si AÎMmxn(R) entonces rangA£min(m,n).Se dice que tiene rango máximo si rangA=min(m,n).

ii) rangA=rangAt.

iii)AÎMn(R) es inversible (|A|¹0)ÛrangA=n.

iv) Sea AÎMmxn(R), si se intercambian dos filas (resp., dos columnas) de A o se multiplica una fila (resp. columna) por un escalar no nulo, o se suma a una fila (resp. columna) otra fila (resp. columna) multiplicada por un escalar, entonces el rango de la matriz resultante no varía.

v) Si una matriz se transforma en triangular superior (inferior) con elementos no nulos en la diagonal, por medio de operaciones elementales, el rango es el número de filas (columnas) que no son comple-tamente nulas al final de la triangularización.

Sistemas de Ecuaciones Lineales

En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

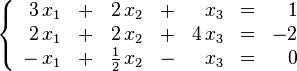
Dos sistemas de ecuaciones se dicen equivalentes si ambos poseen el mismo conjunto de

soluciones, o ambos son incompatibles.

Propiedades

i) Si se intercambian de posición dos ecuaciones, o, se multiplica una ecuación por un número real

no nulo, o, se le suma a una ecuación otra multiplicada por un número real, el sistema resultante es

equivalente. En otras palabras: Si aplicamos operaciones elementales fila a la matriz ampliada de

un sistema obtenemos matrices ampliadas asociadas a un sistema equivalente.

ii) Si tenemos un sistema con menor número de ecuaciones que de incógnitas (m<n), el sistema

es compatible indeterminado o incompatible, y en ningún caso compatible determinado.

iii) Si tenemos un sistema compatible determinado con mayor número de ecuaciones que de

incógnitas (m>n), siempre existirá un sistema equivalente cuadrado, es decir, con igual número

de ecuaciones que de incógnitas, que se puede obtener eligiendo aquellas n ecuaciones del

sistema dado correspondientes a n filas de la matriz ampliada linealmente independientes (esto

es, que contengan una submatriz cuadrada de orden n con determinante no nulo).

iv) Cualquier sistema compatible indeterminado con mayor o igual número de ecuaciones que

de incógnitas (m³n) tiene un sistema equivalente con menor número de ecuaciones que de

incógnitas, exactamente con h ecuaciones si RangA=RangA*=h, obtenible escogiendo h ecuaciones

correspondientes a h filas de la matriz ampliada linealmente independientes (con una

submatriz cuadrada de orden h con determinante no nulo).

v) Dado el sistema AX=B, siendo AÎMn(R) (sist. cuadrado, de n ec. y n incóg.) con |A|¹0 (sist.

compatible determinado), BÎMnx1(R), B¹0, su solución puede venir dada de las dos siguientes

formas equivalentes:

 Forma de la Regla de Cramer X=A-1×BÎMnx1(R)