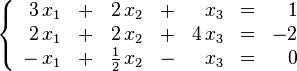9ª HORA DE OPEN COURSE

En mi 9ª hora de open course e podido ver el siguiente contenido:

FORMAS CUADRÁTICAS

Dada una matriz (IR) n AÎM , se define la FORMA CUADRÁTICA real asociada a la matriz

A a la función : IR IR n Q ® dada por Q(x) x Ax T = para todo n

una forma cuadrática es una expresión polinómica en n variables cuyos términos son todos de grado dos.

CLASIFICACIÓN DE FORMAS CUADRÁTICAS

Dada una matriz simétrica (IR) n AÎM , se dice que la Forma Cuadrática asociada a A es (y del mismo modo,

se dice que la matriz A es):

· Definida Positiva Û

x Ax > 0 T para todo IR , 0 n xÎ x ¹

· Semidefinida Positiva Û

x Ax ³ 0 T para todo n xÎIR

· Definida Negativa Û

x Ax < 0 T para todo IR , 0 n xÎ x ¹

· Semidefinida Negativa Û

x Ax £ 0 T para todo n xÎIR

· Indefinida Û

no es Semidefinida Positiva ni Semidefinida Negativa

Proposición 4.1: Dada una matriz simétrica (IR) n AÎM , siendo Ai el determinante de la submatriz de orden i

que se forma sobre la diagonal principal de A empezando en su primer elemento a11, se tiene:

· Si 0, 0, , 0 0 1 2 1 > > > ³ n- n A A K A y A Þ A Semidefinida Positiva

· Si 0, 0, , 1 2 A < A > K (alterna el signo) pudiendo anularse sólo n A Þ A Semidefinida Negativa

Particularmente,

0, 0, , 0 0 1 2 1 > > > > n- n A A K A y A Û A Definida Positiva

0, 0, , 1 2 A < A > K (alterna el signo) Û A Definida Negativa

Página 2 de 2

· Si no se verifica 0, 0, , 0 1 2 ³ ³ ³ n A A K A ni 0, 0, , 1 2 A £ A ³ K (alterna el signo) Þ A Indefinida

CLASIFICACIÓN DE FORMAS CUADRÁTICAS RESTRINGIDAS

La Forma Cuadrática Q restringida a S asociada a la matriz A es (esto es, se dice que Q restringida a S es):

· Definida Positiva Û

x Ax > 0 T para todo xÎS, x ¹ 0

· Semidefinida Positiva Û

x Ax ³ 0 T para todo xÎS

· Definida Negativa Û

x Ax < 0 T para todo xÎS, x ¹ 0

· Semidefinida Negativa Û

x Ax £ 0 T para todo xÎS

· Indefinida Û

no es Semidefinida Positiva ni Semidefinida Negativa.

8ª HORA DE OPEN COURSE

En mi 8ª hora de open course e podido ver los siguientes contenidos:


RANGO DE UNA MATRIZ

Se define el rango de una matriz AÎMmxn(R) (rangA) por una de las siguientes definiciones equi-valentes:

a) Es el orden de la mayor submatriz cuadrada de A con determinante no nulo.

b) Es el mayor número de filas de A linealmente independientes.

c) Es el mayor número de columnas de A linealmente independientes.

Propiedades

i) Si AÎMmxn(R) entonces rangA£min(m,n).Se dice que tiene rango máximo si rangA=min(m,n).

ii) rangA=rangAt.

iii)AÎMn(R) es inversible (|A|¹0)ÛrangA=n.

iv) Sea AÎMmxn(R), si se intercambian dos filas (resp., dos columnas) de A o se multiplica una fila (resp. columna) por un escalar no nulo, o se suma a una fila (resp. columna) otra fila (resp. columna) multiplicada por un escalar, entonces el rango de la matriz resultante no varía.

v) Si una matriz se transforma en triangular superior (inferior) con elementos no nulos en la diagonal, por medio de operaciones elementales, el rango es el número de filas (columnas) que no son comple-tamente nulas al final de la triangularización.

Sistemas de Ecuaciones Lineales

En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

Dos sistemas de ecuaciones se dicen equivalentes si ambos poseen el mismo conjunto de

soluciones, o ambos son incompatibles.

Propiedades

i) Si se intercambian de posición dos ecuaciones, o, se multiplica una ecuación por un número real

no nulo, o, se le suma a una ecuación otra multiplicada por un número real, el sistema resultante es

equivalente. En otras palabras: Si aplicamos operaciones elementales fila a la matriz ampliada de

un sistema obtenemos matrices ampliadas asociadas a un sistema equivalente.

ii) Si tenemos un sistema con menor número de ecuaciones que de incógnitas (m<n), el sistema

es compatible indeterminado o incompatible, y en ningún caso compatible determinado.

iii) Si tenemos un sistema compatible determinado con mayor número de ecuaciones que de

incógnitas (m>n), siempre existirá un sistema equivalente cuadrado, es decir, con igual número

de ecuaciones que de incógnitas, que se puede obtener eligiendo aquellas n ecuaciones del

sistema dado correspondientes a n filas de la matriz ampliada linealmente independientes (esto

es, que contengan una submatriz cuadrada de orden n con determinante no nulo).

iv) Cualquier sistema compatible indeterminado con mayor o igual número de ecuaciones que

de incógnitas (m³n) tiene un sistema equivalente con menor número de ecuaciones que de

incógnitas, exactamente con h ecuaciones si RangA=RangA*=h, obtenible escogiendo h ecuaciones

correspondientes a h filas de la matriz ampliada linealmente independientes (con una

submatriz cuadrada de orden h con determinante no nulo).

v) Dado el sistema AX=B, siendo AÎMn(R) (sist. cuadrado, de n ec. y n incóg.) con |A|¹0 (sist.

compatible determinado), BÎMnx1(R), B¹0, su solución puede venir dada de las dos siguientes

formas equivalentes:

 Forma de la Regla de Cramer X=A-1×BÎMnx1(R)

7ª HORA DE OPEN COURSE

EN MI 7ª HORA DE OPEN COURSE E VISTO LOS SIGUIENTES CONTENIDOS:


Definición de matriz inversa

Se dice que una matriz cuadrada A es inversible, si existe una matriz B con la propiedad de que

A·B = B·A = I

siendo I la matriz identidad.

Denominamos a la matriz B la inversa de A y la denotamos por A-1.

Una matriz se dice que es inversible o regular si posee inversa. En caso contrario, se dice que es singular. A INVERSA DE UNA MATRIZ

Condición de inversibilidad

El problema de encontrar elementos inversos para el producto de matrices tiene como primer

inconveniente que, para empezar, no siempre dadas dos matrices A y B, que podamos hacer el

producto A·B significa que podamos hacer el producto B·A

Además, que dos matrices sean inversas una de la otra significa, en particular, que el producto ha de dar como resultado la matriz identidad. Si recordamos la definición, la matriz identidad es aquélla cuyos elementos son nulos salvo los de la diagonal, que son 1, y, además, esto es importante, dicha

matriz es cuadrada. El hecho de que la matriz identidad sea cuadrada nos va a restringir mucho el

conjunto de matrices para las que podremos hablar de inversión.

¿Cuándo tiene inversa una matriz?

Una matriz  A  de orden  n  (n filas y n columnas) tiene inversa cuando su rango es  n, es decir, cuando el rango de dicha matriz coincide con su orden.

¿Cómo se puede calcular la inversa de una matriz?

 Básicamente hay tres procedimientos para calcular la inversa de una matriz. Son los siguientes:

1º Aplicando la definición y resolviendo los sistemas de ecuaciones correspondientes. Resulta muy laborioso cuando el orden de la matriz es superior a  2.

2º Por el método de Gauss.

3º Por determinantes y adjuntos (que describiremos en la unidad de determinantes).